Giáo trình Hệ thống điều khiển tự động (Phần 2)

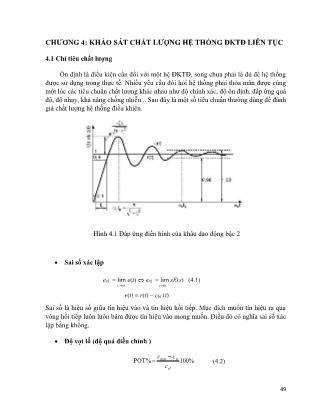
49 
CHƯƠNG 4: KHẢO SÁT CHẤT LƯỢNG HỆ THỐNG ĐKTĐ LIÊN TỤC 
4.1 Chỉ tiêu chất lượng 
Ổn định là điều kiện cần đối với một hệ ĐKTĐ, song chưa phải là đủ để hệ thống 
được sử dụng trong thực tế. Nhiều yêu cầu đòi hỏi hệ thống phải thỏa mãn được cùng 
một lúc các tiêu chuẩn chất lượng khác nhau như độ chính xác, độ ổn định, đáp ứng quá 
độ, độ nhạy, khả năng chống nhiễu... Sau đây là một số tiêu chuẩn thường dùng để đánh 
giá chất lượng hệ thống điều khiển. 
 Hình 4.1 Đáp ứng điển hình của khâu dao động bậc 2 
• Sai số xác lập 
exl = lim e(t) exl = lim sE(s) (4.1) 
t →0 s→0 
 e(t) = r(t) − cht (t) 
Sai số là hiệu số giữa tín hiệu vào và tín hiệu hồi tiếp. Mục đích muốn tín hiệu ra qua 
vòng hồi tiếp luôn luôn bám được tín hiệu vào mong muốn. Điều đó có nghĩa sai số xác 
lập bằng không. 
• Độ vọt lố (độ quá điều chỉnh ) 
 100%POT% max
xl
xl
c
cc −
= (4.2) 
50 
• Thời gian đáp ứng 
• Thời gian lên đỉnh là thời gian đáp ứng ra đạt giá trị cực đại (tp = tpeak). 
• Thời gian quá độ ts = tset xác định bởi thời điểm đáp ứng ra từ sau đó trở đi không vượt 
ra khỏi miền giới hạn sai số quanh giá trị xác lập. Ví dụ: có thể là ± 2%, ± 5%... 
• Độ dữ trữ ổn định 
Định nghĩa: Khoảng cách từ trục ảo đến nghiệm cực gần nhất (nghiệm thực hoặc phức) 
được gọi là độ dữ trữ ổn định của hệ. Ký hiệu khoảng cách ngắn nhất ấy là λ0, nếu λ0 
càng lớn thì quá trình quá độ càng nhanh về xác lập. Đáp ứng quá độ của hệ bậc n: 
1
)(
1
00 eeec(t)
n
i
tp
i
t
n
i
tp
i
ii 
=
+−
=
==   (4.3) 
trong đó Re (pi +λ0 ) <= 0 
• Tiêu chuẩn tích phân 
Trong thực tế một hệ thống ĐKTĐ được thiết kế phải thỏa yêu cầu ở cả hai chế độ xác 
lập và quá độ. Quá trình quá độ có thể được đánh giá thông qua giá trị tích phân của sai 
lệch giữa giá trị đặt và giá trị tức thời đo được của đại lượng cần điều chỉnh. 
4.2. Sai số xác lập 
Xét hệ thống hồi tiếp âm có sơ đồ khối như hình vẽ: 
 Hình 4.2 Hệ thống hối tiếp âm 
Sai số của hệ thống là: 
51 
Sai số xác lập: 
 (4.4) 
Sai số xác lập không những phụ thuộc vào cấu trúc và thông số của hệ thống mà còn 
phụ thuộc vào tín hiệu vào. 
4.2.1 Tín hiệu vào là hàm nấc đơn vị 
 (4.5) 
4.2.2 Tín hiệu vào là hàm dốc đơn vị 
 (4.6) 
4.2.3 Tín hiệu vào là hàm parabol 
 (4.7) 
52 
Nhận xét: 
Tùy theo số khâu tích phân lý tưởng có trong hàm truyền hở G( s) H(s) mà Kp , Kv , Ka 
có giá trị như bảng sau: 
Số khâu tích phân Hệ số vị trí Hệ số vận tốc Hệ số gia tốc 
trong G(s)H(s) K P KV K a 
0 K P < 0 0 
1 KV < 0 
2 K a < 
>3 
- Nếu G(s)H(s) không có khâu tích phân lý tưởng thì hệ thống kín theo kịp sự thay đổi 
của tín hiệu vào là hàm nấc với sai số: 
 𝑒𝑥𝑙 =
1
1+𝐾𝑝
và không theo kịp sự thay đổi của tín hiệu vào là hàm dốc và hàm parabol. 
- Nếu G(s)H(s) có một khâu tích phân lý tưởng thì hệ thống kín theo kịp sự thay đổi của 
tín hiệu vào là hàm nấc với sai số exl = 0, và theo kịp sự thay đổi của tín hiệu vào là hàm 
dốc với sai số: 
𝑒𝑥𝑙 =
1
𝐾𝑣
và không theo kịp sự thay đổi của tín hiệu vào là hàm parabol, hệ thống có một khâu 
tích phân lý tưởng gọi là hệ vô sai bậc một. 
- Nếu G(s)H(s) có hai khâu tích phân lý tưởng thì hệ thống kín theo kịp sự thay đổi của 
tín hiệu vào là hàm nấc và hàm dốc với sai số exl = 0, theo kịp sự thay đổi của tín hiệu 
vào là hàm parabol với sai số: 
a
xl
K
e
1
= , hệ thống có hai khâu tích phân lý tưởng gọi 
là hệ vô sai bậc hai. 
- Nếu G(s)H(s) có ba khâu tích phân lý tưởng thì hệ thống kín theo kịp sự thay đổi của 
tín hiệu vào là hàm nấc, hàm dốc và hàm parabol với sai số exl =0, hệ thống có ba khâu 
tích phân lý tưởng gọi là hệ vô sai bậc ba. 
- Hệ thống có n khâu tích phân lý tưởng gọi là hệ vô sai bậc n. 
53 
4.3 Đáp ứng quá độ 
Đáp ứng quá độ là đáp ứng của hệ thống khi tín hiệu vào là hàm nấc đơn vị. 
4.3.1 Hệ quán tính bậc một 
Hàm truyền: 
Hệ thống kín chỉ có một cực thực 
 Hình 4.3. Giản đồ cực - zero của hệ quán tính bậc nhất 
Hình 4.4.Đáp ứng quá độ của hệ quán tính bậc nhất 
54 
Đáp ứng của hệ thống khi tín hiệu vào là hàm nấc: 
Nhận xét: (hình 4.4) 
• Đáp ứng quá độ của khâu quán tính bậc nhất không có vọt lố. 
• Thời hằng T là thời điểm c(t) đạt 63.2% giá trị xác lập, T càng nhỏ đáp ứng càng nhanh. 
• Thời gian xác lập ts (settling time) là thời gian để sai số giữa c(t) và giá trị xác lập nhỏ 
hơn ε (ε = 5% hay 2%). 
• Sai số xác lập bằng 0. 
4.3.2 Hệ dao động bậc hai 
Hàm truyền: 
trong đó: 
Hệ thống có cặp cực phức liên hợp 
55 
Hình 4.5 Giản đồ cực - zero của hệ dao động bậc hai 
Hình 4.6 Đáp ứng quá độ của hệ dao động bậc hai 
Đáp ứng của hệ thống khi tín hiệu vào là hàm nấc 
trong đó độ lệch pha ө xác định bởi θ = ξ 
Nhận xét: (hình 4.6) 
• Đáp ứng quá độ của khâu dao động bậc hai có dạng dao động với biên độ giảm dần. 
 - Nếu  = 0: c(t) = 1- sinnt, đáp ứng của hệ là dao động không suy giảm với tần số 
ωn, ωn gọi là tần số dao động tự nhiên. 
56 
- Nếu 0 <ξ <1, đáp ứng của hệ là dao động với biên độ giảm dần, ξ gọi là hệ số tắt, ξ 
càng lớn dao động suy giảm càng nhanh. 
• Đáp ứng của khâu dao động bậc hai có vọt lố. 
Tổng quát, độ vọt lố (POT – Percent of Overshoot) được định nghĩa là 
 (4.8) 
(cmax - giá trị cực đại của c(t); cxl - giá trị xác lập của c(t)) 
Đối với hệ dao động bậc hai, độ vọt lố POT được tính bởi công thức 
 (4.9) 
• Thời gian xác lập ts là thời gian để sai số giữa c(t) và giá trị xác lập nhỏ hơn e (e = 
5% hay 2%). 
Đối với hệ bậc hai 
 (4.10) 
 (4.11) 
• Thời gian lên tr (rise time) là thời gian để c(t) tăng từ 10% đến 90% giá trị xác lập. 
Đối với hệ bậc hai 
 (4.12) 
Chú ý: Nếu ξ ≥1, ta không gọi là hệ dao động bậc hai vì trong trường hợp này đáp ứng 
của hệ không có dao động. 
• Nếu ξ =1, hệ thống kín có một nghiệm kép (thực). 
57 
Đáp ứng của hệ thống 
• Nếu ξ>1, hệ thống kín có hai nghiệm thực phân biệt 
Đáp ứng của hệ thống 
58 
4.3.3 Hệ bậc cao 
Hình 4.7 Cặp cực quyết định của hệ bậc cao 
Hệ bậc cao có nhiều hơn hai cực. Đáp ứng tương ứng với các cực nằm càng xa trục ảo 
suy giảm càng nhanh. Do đó có thể xấp xỉ hệ bậc cao về hệ bậc hai với cặp cực là hai 
cực nằm gần trục ảo nhất. Cặp cực nằm gần trục ảo nhất của hệ bậc cao gọi là cặp cực 
quyết định. 
4.4 Các tiêu chuẩn tối ưu hóa đáp ứng quá độ 
• Tiêu chuẩn tích phân sai lệch IE (Integrated Error) 
Đối với hệ có đáp ứng quá độ không dao động (đường 1 hình 5.8) thì tiêu chuẩn IE chính 
là diện tích của hàm sai lệch e(t) tạo với trục thời gian t cần đạt giá trị cực tiểu thì chất 
lượng đạt tốt nhất. 
59 
 Hình 4.8 Tiêu chuẩn IE và IAE 
Song đối với hệ có đáp ứng quá độ dao động ổn định (đường 2) thì tiêu chuẩn IE không 
phản ánh đúng chất lượng của hệ thống do có miền diện tích âm đã được trừ bớt đi. Kết 
quả giá trị tích phân nhỏ nhưng quá trình quá độ xấu. Vì vậy phải sử dụng tiêu chuẩn 
tích phân trị số tuyệt đối của sai lệch. 
• Tiêu chuẩn IAE (Integral of the Absolute Magnitude of the Error - 
tích phân trị tuyệt đối biên độ sai số) 
 (4.13) 
Đối với hệ bậc hai: 
• Tiêu chuẩn ISE (Integral of the Square of the Error - tích phân của 
bình phương sai số) 
 (4.14) 
ISE xem nhẹ những diện tích bé vì bình phương một số nhỏ hơn 1 bé hơn trị số tuyệt đối 
của số ấy. Một trong những lý do khiến tiêu chuẩn ISE thường được sử dụng là công 
việc tính toán và thực hiện đơn giản. Có thể tính ước lượng ISE theo biến đối Fourier 
60 
hoặc theo công thức. 
Đối với hệ bậc hai: 
• Tiêu chuẩn ITAE (Integral of Time multiplied by the Absolute Value of the 
Error- tích phân của thời gian nhân với trị tuyệt đối của sai số) 
 (4.15) 
Đối với hệ bậc hai: 
Trong ba tiêu chuẩn tối ưu hóa đáp ứng quá độ vừa trình bày ở trên, tiêu chuẩn ITAE 
được sử dụng nhiều nhất. Để đáp ứng quá độ của hệ thống bậc n là tối ưu theo chuẩn 
ITAE thì mẫu số hàm truyền kín hệ bậc n phải có dạng 
Bậc Mẫu số hàm truyền 
1 s +  n 
2 
s 
2 2 
 +1.414n s + n 
3 
s 
3 
+1.75n s 
2 2 3 
 + 2.15n s + n 
4 s 
4 
+ 2.1n s 
3 
+ 
 2 2 3 4 
 3.4n s + 2.7n s + n 
Nếu mẫu số hàm truyền hệ kín có dạng như trên và tử số hàm truyền hệ kín của hệ bậc 
n là ωnn thì đáp ứng quá độ của hệ thống là tối ưu và sai số xác lập bằng 0. 
• Tiêu chuẩn tích phân có tính đến ảnh hưởng của tốc độ thay đổi của sai lệch 
e(t) 
với α là hằng số được chọn thích hợp cho từng trường hợp. 
Ví dụ: α lớn không cho phép dao động lớn. Ngược lại, α nhỏ cho phép quá độ dao động 
lớn. 
61 
Câu hỏi ôn tập chương 4 
1. Ý nghĩa của việc phân tích chất lượng quá độ của hệ thống trong thiết kế hệ thống tự 
động? 
2. Phương pháp phân tích đáp ứng quá độ của hệ thống bậc cao? 
3. Ý nghĩa của đáp ứng quá độ? 
4. Nêu các tiêu chuẩn tích phân thường sử dụng. 
5. Cho ví dụ về đáp ứng quá độ yêu cầu của một số hệ thống/ quá trình đã phân tích? 
62 
CHƯƠNG 5: TỔNG HỢP HỆ THỐNG ĐKTĐ LIÊN TỤC 
5.1 Khái niệm 
Thiết kế là toàn bộ quá trình bổ sung các thiết bị phần cứng cũng như thuật toán phần 
mềm vào hệ cho trước để được hệ mới thỏa mãn yêu cầu về tính ổn định, độ chính xác, đáp 
ứng quá độ,  Có nhiều cách bổ sung bộ điều khiển vào hệ thống cho trước, trong khuôn khổ 
bài giảng này chúng ta chủ yếu xét hai cách sau: 
Cách 1: thêm bộ điều khiển nối tiếp với hàm truyền của hệ hở, phương pháp này gọi là hiệu 
chỉnh nối tiếp (H5.1). Bộ điều khiển được sử dụng có thể là bộ hiệu chỉnh sớm pha, trễ pha, 
sớm trễ pha, P, PD, PI, PID, Để thiết kế hệ thống hiệu chỉnh nối tiếp chúng ta có thể sử 
dụng phương pháp QĐNS hay phương pháp biểu đồ Bode. Ngoài ra một phương pháp cũng 
thường được sử dụng là thiết kế theo đặc tính quá độ chuẩn. 
 Hình 5.1 Hệ thống hiệu chỉnh nối tiếp 
Cách 2: điều khiển hồi tiếp trạng thái, theo phương pháp này tất cả các trạng thái của hệ thống 
được phản hồi trở về ngõ vào và tín hiệu điều khiển có dạng: 
 u(t) = r(t) - Kx(t) 
(H.5.2). Tùy theo cách tính véctơ hồi tiếp trạng thái K mà ta có phương pháp điều 
khiển phân bố cực, điều khiển tối ưu LQR, . 
 Hình 5.2 Hệ thống điều khiển hồi tiếp trạng thái 
Quá trình thiết kế hệ thống là quá trình đòi hỏi tính sáng tạo do trong khi thiết kế thường có 
nhiều thông số phải chọn lựa. 
Người thiết kế cần thiết phải hiểu được ảnh hưởng của các khâu hiệu chỉnh đến chất lượng 
của hệ thống và bản chất của từng phương pháp thiết kế thì mới có thể thiết kế được hệ thống 
63 
có chất lượng tốt. Do đó các phương pháp thiết kế trình bày trong chương này chỉ mang tính 
gợi ý, đó là những cách thường được sử dụng chứ không phải là phương pháp bắt buộc phải 
tuân theo. 
Việc áp dụng một cách máy móc thường không đạt được kết quả mong muốn trong thực tế. 
Dù thiết kế theo phương pháp nào yêu cầu cuối cùng vẫn là thỏa mãn chất lượng mong muốn, 
cách thiết kế, cách chọn lựa thông số không quan trọng. 
Trước khi xét đến các phương pháp thiết kế bộ điều khiển, chúng ta xét ảnh hưởng của các bộ 
điều khiển đến chất lượng của hệ thống. 
5.2 Các phương pháp hiệu chỉnh hệ thống 
Nguyên tắc thiết kế hệ thống dùng phương pháp hiệu chỉnh thông số hay còn gọi là 
QĐNS là dựa vào phương trình đặc tính của hệ thống sau khi hiệu chỉnh: 
 1+Gc(s)G(s)=0 (5.1) 
 (5.2) 
Ta cần chọn thông số của bộ điều khiển Gc(s) sao cho phương trình (5.1) có nghiệm tại vị trí 
mong muốn. 
5.2.1 Hiệu chỉnh sớm pha 
Để thuận lợi cho việc vẽ QĐNS chúng ta biểu diễn hàm truyền khâu hiệu chỉnh sớm pha dưới 
dạng sau : 
 (5.3) 
Bài toán đặt ra là chọn giá trị KC, a và T để đáp ứng của hệ thống thỏa mãn yêu cầu về chất 
lượng quá độ (độ vọt lố, thời gian xác lập, ) 
5.2.2 Hiệu chỉnh trễ pha 
Hàm truyền khâu hiệu chỉnh trễ pha cần thiết kế có dạng: 
64 
Bài toán đặt ra là chọn giá trị KC, β và T để đáp ứng của hệ thống thỏa mãn yêu cầu về sai số 
xác lập mà “không” làm ảnh hưởng đến đáp ứng quá độ (ảnh hưởng không đáng kể). 
Ta đã biết do khâu hiệu chỉnh trễ pha có hệ số khuếch đại ở miền tần số thấp lớn nên có 
tác dụng làm giảm sai số xác lập của hệ thống. Để đáp ứng quá độ của hệ thống sau khi hiệu 
chỉnh trễ pha gần như không đổi thì cặp cực quyết định của hệ thống trước và sau khi hiệu 
chỉnh phải nằm rất gần nhau. 
5.2.3 Hiệu chỉnh sớm trễ pha 
Hàm truyền khâu hiệu chỉnh sớm trễ pha cần thiết kế có dạng: 
 Gc(s) = Gc1(s).Gc2(s) 
trong đó: GC1 (s) là khâu hiệu chỉnh sớm pha và GC2(s) là khâu hiệu chỉnh trễ pha. 
5.3 Thiết kế hệ thống điều khiển PID 
Bộ điều khiển PID là trường hợp đặc biệt của hiệu chỉnh sớm trễ pha nên về nguyên tắc 
có thể thiết kế bộ điều khiển PID bằng phương pháp dùng QĐNS hoặc dùng biểu đồ Bode. 
Một phương pháp khác cũng thường dùng để thiết kế bộ điều khiển PID là phương pháp giải 
tích. Sau đây là một ví dụ: 
Ví dụ 5.3. Cho hệ thống điều khiển như hình vẽ: 
Hãy xác định thông số của bộ điều khiển PID sao cho hệ thống thỏa mãn yêu cầu: 
- Hệ có cặp nghiệm phức với ξ= 0,5 , ωn = 8 
- Hệ số vận tốc KV = 100. 
Giải: Hàm truyền bộ điều khiển PID cần thiết kế: 
65 
𝐺𝑐(𝑠) = 𝐾𝑝 +
𝐾𝐼
𝑠
+ 𝐾𝐷𝑠 
Hệ số vận tốc của hệ sau khi hiệu chỉnh: 
Theo yêu cầu đề bài KV = 100 nên suy ra: KI =100 
Phương trình đặc tính của hệ sau khi hiệu chỉnh là: 
 (1) 
Để hệ thống có cặp cực phức với: 
thì phương trình đặc tính (1) phải có dạng: 
Cân bằng các hệ số hai phương trình (1) và (2), suy ra: 
Với KI = 100, giải hệ phương trình trên ta được: 
66 
Vậy hàm truyền của khâu hiệu chỉnh PID cần thiết kế là: 
Bộ điều khiển PID được sử dụng rất rộng rãi trong thực tế để điều khiển nhiều loại đối 
tượng khác nhau như nhiệt độ lò nhiệt, tốc độ động cơ, mực chất lỏng trong bồn chứa... 
do nó có khả năng làm triệt tiêu sai số xác lập, tăng tốc độ đáp ứng quá độ giảm độ vọt lố nếu 
các thông số của bộ điều khiển được chọn lựa thích hợp. Do tính thông dụng của nó nên nhiều 
hãng sản xuất thiết bị điều khiển đã cho ra đời các bộ điều khiển PID thương mại rất tiện 
dụng. Trong thực tế các phương pháp thiết kế bộ điều khiển PID dùng QĐNS, biểu đồ Bode 
hay phương pháp giả tích rất ít được sử dụng do sự khó khăn trong việc xây dựng hàm truyền 
của đối tượng. Phương pháp phổ biến nhất để chọn thông số cho các bộ điều khiển PID thương 
mại hiện nay là phương pháp Zeigler-Nichols. 
• Phương pháp Zeigler-Nichols 
Phương pháp Zeigler-Nichols là phương pháp thực nghiệm để thiết kế bộ điều khiển P, PI, 
hoặc PID bằng cách dựa vào đáp ứng quá độ của đối tượng điều khiển. Bộ điều khiển PID 
cần thiết kế có hàm truyền là: 
 𝐺𝑐(𝑠) = 𝐾𝑝 +
𝐾𝐼
𝑠
+ 𝐾𝐷𝑠 = 𝐾𝑝 (1 +
1
𝑇𝐼𝑠
+ 𝑇𝐷𝑠) (5.4) 
Zeigler và Nichols đưa ra hai cách chọn thông số bộ điều khiển PID tùy theo đặc điểm của 
đối tượng. 
Cách 1: Dựa vào đáp ứng quá độ của hệ hở, áp dụng cho các đối tượng có đáp ứng đối với 
tín hiệu vào là hàm nấc có dạng chữ S như hình 5.3, ví dụ như nhiệt độ lò nhiệt, tốc độ động 
cơ,  
 Hình 5.3 Đáp ứng nấc của hệ hở có dạng S 
Thông số bộ điều khiển P, PI, PID được chọn như sau: 
67 
 Thông số 
Bộ ĐK 
Kp 
 TI 
 TD 
P T2/(T1.K) ∞ 0 
PI 0.9T2/(T1K) T1/0.3 0 
PID 1.2T2/(T1.K) 2T1 0.5T1 
Ví dụ 5.4. Hãy thiết kế bộ điều khiển PID điều khiển nhiệt độ của lò sấy, biết đặc tính quá độ 
của lò sấy thu được từ thực nghiệm có dạng như sau: 
Giải. Dựa vào đáp ứng quá độ thực nghiệm ta có: 
 T1 = 8 min = 480sec 
 T2 = 24 min = 1440sec 
Chọn thông số bộ điều khiển PID theo phương pháp Zeigler- Nichols: 
Kp= 1,2 T2/T1 =1440/480 =3,6 
TI = 2T1 =2x 480 = 960sec 
TD= 0,5T1 = 0,5x480 = 240sec 
Do đó: 
𝐺𝑃𝐼𝐷(𝑠) = 𝐾𝑝(1 +
1
𝑇𝐼𝑠
+ 𝑇𝐷𝑠) = 3,6(1 +
1
960𝑠
+ 240𝑠) 
Cách 2: Dựa vào đáp ứng quá độ của hệ kín, áp dụng cho các đối tượng có khâu tích phân lý 
tưởng, ví dụ như mực chất lỏng trong bồn chứa, vị trí hệ truyền động dùng động cơ,... Đáp 
68 
ứng quá độ (hệ hở) của các đối tượng có khâu tích phân lý tưởng không có dạng như hình 5.3 
mà tăng đến vô cùng. Đối với các đối tượng thuộc loại này ta chọn thông số bộ điều khiển 
PID dựa vào đáp ứng quá độ của hệ kín như hình 5.4. Tăng dần hệ số khuếch đại K của hệ 
kín ở hình 5.4 đến giá trị giới hạn Kgh, khi đó đáp ứng ra của hệ kín ở trạng thái xác lập là 
dao động ổn định với chu kỳ Tgh. 
 Hình 5.4 Đáp ứng nấc của hệ kín khi K = Kgh 
Thông số bộ điều khiển P, PI, PID được chọn như sau: 
 Thông số 
Bộ ĐK 
Kp 
 TI 
 TD 
P 0.5 Kgh ∞ 0 
PI 0.45Kgh 0.83Tgh 0 
PID 0.6Kgh 0.5Tgh 0.125Tgh 
Ví dụ 5.5: Hãy thiết kế bộ điều khiển PID điều khiển vị trí góc quay của động cơ DC, biết 
rằng nếu sử dụng bộ điều khiển tỉ lệ thì bằng thực nghiệm ta xác định được khi K = 20 vị trí 
góc quay động cơ ở trạng thái xác lập là dao động với chu kỳ T = 1 sec. 
69 
Giải. Theo dữ kiện của bài toán, ta có: 
 Kgh=20 ; Tgh=1sec 
Chọn thông số bộ điều khiển PID theo phương pháp Zeigler-Nichols: 
Kp= 0,6Kgh =0,6x20 =12 
TI = 0,5Tgh= 0,5x1= 0,5sec 
TD= 0,125Tgh = 0,125x1= 0,125sec 
Do đó: 
𝐺𝑃𝐼𝐷(𝑠) = 𝐾𝑝(1 +
1
𝑇𝐼𝑠
+ 𝑇𝐷𝑠) = 12(1 +
1
0,5𝑠
+ 0,125𝑠) 
70 
Câu hỏi ôn tập chương 5. 
1. Tại sao phải thiết kế bộ điều khiển cho hệ thống? 
2. Ảnh hưởng của cực và zero tới đáp ứng của hệ thống? 
3. Ảnh hưởng của các khâu bù/ bộ điều khiển tới QĐNS và đáp ứng của hệ thống? 
4. Ảnh hưởng của các khâu bù/ bộ điều khiển tới biểu đồ Bode và đáp ứng của hệ thống? 
5. Các bước cần làm để thiết kế bộ điều khiển cho một đối tượng với các yêu cầu thiết kế 
cho trước nếu đối tượng chưa xác định mô hình toán? 
71 
Phụ lục: Bảng biến đổi Laplace của một số hàm cơ bản 
72 
Tài liệu tham khảo 
[1].Phạm Công Ngô. Lý Thuyết Điều Khiển Tự Động. NXB: Khoa học và kỹ thuật. 2006. 
[2]. Nguyễn Thị Phương Hà. Lý thuyết điều khiển tự động. NXB: ĐHQG Tp HCM. 2005. 
[3]. Katsuhiko Ogata. Model Control Engineering 5th Edition, printed by Prentice Hall 
India. 2009/