Giáo trình Kỹ thuật Anten

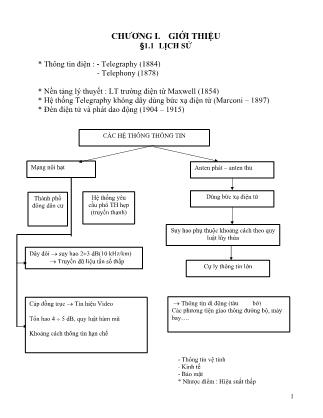
CHƯƠNG I. GIỚI THIỆU 
§1.1 LỊCH SỬ 
* Thông tin điện : - Telegraphy (1884) 
 - Telephony (1878) 
* Nền tảng lý thuyết : LT trường điện từ Maxwell (1854) 
* Hệ thống Telegraphy không dây dùng bức xạ điện từ (Marconi – 1897) 
* Đèn điện tử và phát dao động (1904 – 1915) 
Mạng nội hạt Anten phát – anten thu 
Thành phố 
đông dân cư 
Hệ thống yêu 
cầu phổ TH hẹp 
(truyền thanh) 
Dùng bức xạ điện từ 
Suy hao phụ thuộc khoảng cách theo quy 
luật lũy thừa 
Cự ly thông tin lớn 
Dây đôi → suy hao 2÷3 dB(10 kHz/km) 
 → Truyền dữ liệu tần số thấp 
Cáp đồng trục → Tín hiệu Video 
Tổn hao 4 ÷ 5 dB, quy luật hàm mũ 
Khoảng cách thông tin hạn chế 
 → Thông tin di động (tàu bờ) 
Các phương tiện giao thông đường bộ, máy 
bay. 
CÁC HỆ THỐNG THÔNG TIN 
 1
- Thông tin vệ tinh 
- Kinh tế 
- Bảo mật 
* Nhược điểm : Hiệu suất thấp 
§1.2 CÁC HỆ THỐNG ANTEN 
+ Anten thông dụng : - Anten râu trên ôtô 
- Anten tai thỏ trên tivi 
- Anten vòng cho UHF 
- Anten Log-chu kỳ cho TV 
- Anten Parabol thu sóng vệ tinh 
+ Trạm tiếp sóng vi ba (Microwave Relay) 
- Anten mặt 
- Anten Parabol bọc nhựa 
+ Hệ thống thông tin vệ tinh : 
- Hệ anten loa đặt trên vệ tinh 
- Anten chảo thu sóng vệ tinh 
- Mảng các loa hình nón chiếu xạ (20-30GHz) 
+ Anten phục vụ nghiên cứu khoa học 
 QUY ƯỚC VỀ CÁC DẢI TẦN SỐ 
Dải tần số Tên, ký hiệu Ứng dụng 
3 – 30 kHz Very low freq. (VLF) Đạo hàng, định vị 
30 – 300kHz Low freq. (LF) Pha vô tuyến cho mục đích đạo 
hàng 
300 –
3000kHz 
Medium freq. (MF) Phát thanh AM, hàng hải, trạm 
thông tin duyên hải, chỉ dẫn tìm 
kiếm 
3 – 30 MHz High Freq. (HF) Điện thoại, điện báo, phát thanh 
sóng ngắn, hàng hải, hàng không 
30 – 300MHz Very High Freq. (VHF) TV, phát thanh FM, điều khiển 
giao thông, cảnh sát, taxi, đạo 
hàng 
0,3 – 3 GHz Ultrahigh (UHF) TV, thông tin vệ tinh, do thám, 
Radar giám sát, đạo hàng 
3 – 30 GHz Superhigh freq. (SHF) Hàng không, Viba (microwave 
links), thông tin di động, thông 
tin vệ tinh 
30 – 300GHz Extremly high freq. 
(EHF) 
Radar, nghiên cứu khoa học 
 2
§1.3 KHÁI QUÁT VỀ TRUYỀN SÓNG ĐIỆN TỪ 
+ Dải phát thanh AM chuẩn (0,55 – 1,6 MHz): Dùng tháp anten 
+ Dải sóng dài : 
- Anten đơn giản với độ lợi thấp, đặt trên mặt đất. 
- Mode truyền: sóng mặt, suy hao ~ R-4. 
- Mức nhiễu cao do nhiễu công nghiệp 
- Cần máy phát công suất lớn (50-500kW) 
- Mức nhiễu và suy hao cao 
- Cự ly thông tin cỡ vài trăm dặm 
- Suy hao tăng nhanh theo tần số (không sử dụng cho TS>20MHz) 
- Chiều cao của anten cần được lựa chọn thích hợp. 
- Có thể có hiện tượng Fading trong thời gian hàng giây, phút, chịu ảnh 
hưởng của nhiệt độ và độ ẩm không khí. Æ khắc phục FadingÆ phân 
tập theo không gian và tần số. 
+ Dải sóng 30 – 40 MHz : 
- Có thể sử dụng sự phản xạ từ tầng điện ly 
- Cự ly thông tin hàng ngàn km Æ các dịch vụ truyền thông quốc tế 
- Sự phản xạ phụ thuộc mật độ điện tử tạo bởi bức xạ mặt trời 
- Không được sử dụng trên 40MHz (do xuyên qua và fading) 
+Trên 40MHz 
- Truyền thẳng (TV, Viba) 
- Kích thước anten phải lớn gấp một số lần bước sóng 
- Ở dải sóng Viba ( 3 – 30cm) có thể dùng những anten gương có độ lợi cao 
(40-50dB), công suất máy phát giảm, nhiễu khí quyển giảm, có thể dùng 
tín hiệu biên độ nhỏ 
+ Dải sóng mm : 
- Suy giảm sóng do khí quyển hoặc do mưa tăng 
- Cự ly thông tin bị giới hạn 
 3
CHƯƠNG 2 
CƠ SỞ LÝ THUYẾT AN TEN, CÁC THÔNG SỐ CƠ BẢN CỦA ANTEN 
§2.1 MỞ ĐẦU 
Một số qui ước về ký hiệu: chữ nét đậmÆvector, chữ nghiêngÆthông số 
+ Định nghĩa anten: là một cấu trúc được làm từ những vật liệu dẫn điện tốt, được 
thiết kế để có hình dạng kích thước sao cho có thể bức xạ sóng điện từ theo một kiểu 
nhất định một cách hiệu quả. 
+ Nguyên lý hoạt động: dòng điện thay đổi theo thời gian trên bề mặt anten → bức 
xạ sóng điện từ 
Æ Anten là một cấu trúc mà dòng thay đổi theo thời gian, được cấp từ một nguồn 
thích hợp qua đường truyền hoặc ống dẫn sóng, có thể bị kích thích với biên độ lớn 
trên bề mặt anten. 
+ Yêu cầu về cấu trúc anten: đơn giản, kinh tế (ví dụ : anten nửa sóng) 
+ Bài toán chính của lý thuyết và kỹ thuật anten: xác định phân bố mật độ dòng 
điện J trên bề mặt anten sao cho trường bức xạ thỏa mãn các điều kiện biên trên 
anten. Bài toán này thường chỉ có thể giải gần đúng. 
+ Phân bố dòng trên anten có thể được xác định chính xác hơn khi xác định được đặc 
trưng trở kháng của anten. 
+ Từ đặc tính tuyến tính của hệ phơng trình Maxwell, về nguyên tắc có thể xác định 
được phân bố trường tổng khi biết phân bố trường của phân tử dòng. 
+ Các phương trình Maxwell, thế vector và thế vô hướng là những công cụ toán học 
chủ yếu để giải bài toán về anten. 
+ Các đặc trưng cơ bản của một anten: 
- Kiểu bức xạ (hàm phương hướng). 
- Độ rộng tia, hệ số định hướng, điện trở bức xạ. 
+ Các phần tử bức xạ cơ bản: Phần tử dòng điện nguyên tố, vòng điện nguyên tố, 
dòng từ nguyên tố, vòng từ nguyên tố. 
 4
§2.2 PHƯƠNG TRÌNH MAXWELL VÀ CÁC ĐIỀU KIỆN BIÊN 
2.2.1 HỆ PHƯƠNG TRÌNH MAXWELL 
+ Đối tượng chủ yếu của thuyết và kỹ thuật anten là khảo sát sự bức xạ và thu trường 
điều hòa ~ejwt. 
+ Dòng điện và trường sẽ được biểu diễn dưới dạng các vector mà các thành phần 
của chúng là các số phức. Khi đó, trường thực có dạng: 
tjt ωε )e(Re),( rEr = (2.1) 
+ Các phương trình Maxwell: (2.2.a Æe) 
+ Trong chân không : 
ωρ
ρ
ω
ω
j
Dj
j
−=⋅∇
=⋅∇
=⋅∇
+=×∇
−=×∇
J
B
D
JH
BE
0
(2.2a) 
(2.2b) 
(2.2e) 
(2.2d) 
(2.2c) 
 (2.3a);B (2.3a); , 00 ,HE µε ==D 
+ );/(36
10 9
0 metFaraπε
−= )/(10.4 70 metHenry−= πµ
+ Trong môi trường có hằng số điện môi ε và độ dẫn điện σ: dòng dẫn EJc σ= 
 (2.2b) => ( ) JJH +⎟⎟⎠
⎞
⎜⎜⎝
⎛ +=++=×∇ E
j
jEj ω
σεωσωε 
2.2.2 CÁC ĐIỀU KIỆN BIÊN 
BIÊN CỦA MỘT VẬT DẪN LÝ TƯỞNG (σ = ∞): (2.5) 
Bên trong vật dẫn: E , H = 0 
Trên bề mặt: n x E = 0, n . H = 0 
Mật độ dòng điện mặt: sJ = n x H 
Mật độ điện tích mặt: Dns .=ρ
BIÊN CỦA MỘT VẬT DẪN KHÔNG LÝ TƯỞNG: Trường điện từ xuyên qua bề mặt với 
biện độ giảm theo hàm mũ: e-z/δ (δ = (2/ωµoσ)1/2 với đồng , δ = 
6.6x10
mS /108.5 7×=σ
-3cm ở tần số 1MHz, và 2.1x10-4cm ở 1GHz (2.7) 
Ví dụ: với đồng, σ = 5.8x107 S/m, δ = 6.6x10-3 cm ở tần số 1MHz, và 
2.1x10-4 cm ở tần số 1GHz. 
Trong đa số các trường hợp thực tế có thể coi trường điện từ không xuyên qua 
các vật dẫn tốt như kim loại. Tuy nhiên, khi tính đến điện trở của các vật dẫn kim loại 
 5
thì cần tính tới tổn hao Joule theo định luật Ohm (tổn hao của đường truyền, ống dẫn 
sóng) 
TÍNH TỔN HAO: 
Từ trường H tạo ra dòng mặt HnJ s ×= ( định luật Ampere) 
Thành phần tiếp tuyến của điện trường liên quan với mật độ dòng điện mặt: 
ss JnZEn ×=× (ĐL Ohm) (2.8) 
Trong đó Zs là trở kháng bề mặt của vật dẫn: ( )
s
s
jZ σδ+= 1 (Ohm/dt) (2.9) 
Bao gồm thành phần thuần trở 1/σδs (điện trở của lớp da có chiều sâu δs) và thành 
phần cảm ứng do sự xuyên qua của từ trường. 
Tổn hao trên đơn vị diện tích được cho bởi phần thực của vector Poynting hướng vào 
vật dẫn tại bề mặt vật dẫn: 
s
sJ
P σδ
2
2
1
= (2.10) 
- Nếu σ = vô cùng, thì chiều sâu lớp da, và do đó trở kháng bề mặt và tổn hao = 0 
- Thường người ta so sánh trở kháng bề mặt với trở kháng của không gian tự do: 
OhmZ 377
2
1
0
0
0 =⎟⎠
⎞⎜⎝
⎛= εµ (2.11)
- Với Cu, tại 1MHz, Zs = 2.6x10-4(1+j) Ohm 
- Kết quả trên có thể áp dụng cho các vật dẫn tốt khác và cho các bề mặt có bán kính 
cong lớn hơn nhiều so với độ sâu lớp da. 
BIÊN GIỮA HAI ĐIỆN MÔI: 
 21 EnEn ×=× , 21 HnHn ×=× , 21 DnDn ×=× 
2.2.3 THẾ VECTOR VÀ THẾ VÔ HƯỚNG 
 Từ (2.2a), (2.2b) và (2.3) => ,020 JjEkE ωµ−=×∇×∇ (2.12) 
Với là số sóng của không gian tự do ( ) 2/1000 εµω=k
- Theo phương trình này điện trường có thể được tìm trực tiếp khi biết phân bố dòng. 
Trong thực tế có thể đơn giản hóa bài toán nhờ thế vectơ A và thế vô hướng Φ : 
Mặt khác bất cứ vectơ nào với zero curl đều có thể biểu diễn dưới dạng gradient của 
một hàm vô hướng. Do đó có thể đặt : 
 AB ×∇= (2.13) 
- Vì 0=×∇×∇ A nên A được gọi là thế vector. 
- Sử dụng công thức của giải tích vector => 
 ( )Φ+∇∇+−=+∇ 000202 . εωµµ jAJAkA (2.14) 
- Để đơn giản ta chọn : Φ−=×∇ 00εωµjA (Điều kiện Lorentz) (2.15) 
- Khi đó (2.14) trở thành : JAkA 0202 µ−=+∇ (2.16) 
- Thay các phương trình (2.14) và (2.15) vào (2.2c) => 
 (2.17) 0202 / ερ−=Φ+Φ∇ k
 6
- Sử dụng điều kiện Lorentz và (2.14) => 
 00/. εωµω jAAjE ∇∇+−= (2.18) 
- Trường hợp nguồn dòng : 
zz aJJ .= thì zz aJJ .= và ( ) zz JAk 0202 µ−=+∇ (2.19) 
§ 2.3 BỨC XẠ CỦA PHẦN TỬ DÒNG ĐIỆN 
- Định nghĩa phần tử dòng điện: dlI thẳng, rất mỏng, rất ngắn. Giả thiết dữ liệu // 
(z). 
- Thế vector chỉ có một thành phần theo phương (z) tuân theo PT (2.19). trong đó 
Jz=I/dS, với dS là tiết diện của phần tử dòng. Thể tích dV<< nên phần tử dòng có thể 
coi như nguồn định xứ tại một điểm. 
- Nguồn đối xứng cầu ÆAz chỉ là hàm của r 
- Với r ≠ 0: 
 0)(1 2022 =+∂
∂
∂
∂
z
z Ak
r
Ar
rr
 (2.20) 
- Thay 
r
Az
Ψ= thì 21 rdr
d
rdr
dAz Ψ−Ψ= và (2.20) trở thành : 
 0202
2
=Ψ+Ψ k
dr
d (2.21) 
- Pương trình dao động điều hoà này có 2 nghiệm : và rjkeC 01 − rjkeC 02
- Nếu chọn nghiệm thứ nhất và tính tới biến thời gian t thì có thể viết: 
 ( ) jwtrjktr eC +−=Ψ 01,
 Lưu ý: 
c
wk = , ( ) 21−= oo EC µ 
 Thì thu được: ( )
( )crtjw
tr eC
−=Ψ 1, ( 2.22) 
- Nhận xét: Phương trình sóng bức xạ với góc pha ban đầu k0r, thời gian trễ r/c 
- Tính C1: Tích phân (2.19) trong thể tích của hình cầu có bán kính ro rất nhỏ, 
viết:(công thức) 
- Lưu ý: dV = r2sin θ dθ dϕ dr và Az là hàm của 1/r. Nếu chọn ro rát nhỏ thì tích 
phân khối của Az sẽ tỷ lệ với r2 và có thể bỏ qua. Tích phân khối của Jz chính là Idl, 
ta có: (ý nghĩa của grad) 
- Lời giải cuối cùng của A
r
 sẽ là: 
z
rjk
a
r
eIdlA πµ 4
0
0
−
= (2.24) 
* Nhận xét: - Thế vector có dạng sóng lan truyền ra không gian với biên độ 
giảm tỷ lệ nghịch với r. 
 7
- Các mặt sóng đồng pha có dạng hình cầu bán kính r, tâm = góc 
toạ độ. 
 - Vận tốc pha = (công thức) 
 - Bước sóng 
f
C
w
C
koo
===
π
πλ
2
2 (2.25) 
Tìm biểu thức của của trường: 
- Sử dụng (2.13) và (2.18) và hệ toạ độ cầu. 
- Biểu diễn A
r
 theo các thành phần trong hệ toạ độ cầu và lưu ý rằng: 
Ta có: ( )Aae
r
IdlA r
jkt sina-Acos
4
00 θπ
µ −= (2.26) 
Dùng (2.13): 
 ϕπ
θ
µ aerr
jkIdAH rjk02
0
0
1
4
sin.1 −⎟⎠
⎞⎜⎝
⎛ +=×∇= l (2.27) 
Từ (2.18) => θθεωµω aEaEj
AAjE rr +=∇∇+−=
00
.
 (2.28) 
- Nếu r rất lớn so với bước sóng thì : (vùng xa) bỏ qua các số 2
1
r
, 3
1
r
 θπθ ar
ekIdjZE
rjk
4
sin
0
00
−
= l (2.29a) 
 ϕπθ ar
ekjIdH
rjk
4
sin
0
0
−
= l (2.29b) 
* Nhận xét: 
- Vậy ở khu xa, trường bức xạ chỉ có thành phần ngang, điện trường và từ trưòng 
vuông góc với nhauvà vuông góc với phương truyền sóng. tỷ số biên độ của chúng 
chính bằng trở kháng sóng của không gian tự do Z0; 
2
1
0
0
0 ⎟⎠
⎞⎜⎝
⎛= εµZ 
- Dạng vector: 
 HaZE r ×−= 0 (2.30a) 
 EaYH r ×= 0 (2.30b) 
Trong đó: 100 Z=Y
- Trường không có tính đối xứng cầu. ( E Z và H phụ thuộc θsin ) 
* Vector Poynting phức: 
 ( ) 2222020** 32sin.2
1
r
akdZIIHE rπθl=× (2.31b) 
 8
Có dạng thuần thực, (trường bức xạ) có hướng trùng với hướng lan truuyền, và 
công suất bức xạ giảm tỷ lệ nghịch với r2 
* Các số hạng còn lại của (2.27) và (2.28): chiếm ưu thế khi r < λo và tạo ra 
trường phản ứng ở khu gần vì tính thuần ảo của vector Poynting. 
- Nếu kor rất nhỏ sao cho có thể thay thì: (khu gần) 10 ≅− rjke
 ϕπ
θ a
r
kIdH
4
sin0l= (2.32a) 
 ⎥⎦
⎤⎢⎣
⎡
⎟⎟⎠
⎞
⎜⎜⎝
⎛ ++⎟⎟⎠
⎞
⎜⎜⎝
⎛ += θθθπ arjkrarjkr
IdZE r
0
2
0
2
0 11sin11cos2
4
l
 (2.32b) 
Cho k0rphương trình (2.32b) trở thành 
 ⎥⎦
⎤⎢⎣
⎡ += θθθπ arar
QdE r 3
sincos2
4 3
l
 (2.32c) 
Lưu ý : - Tương tự như phân bố trường tĩnh của một dipole điện. 
 - Mặc dù trường ở khu gần không đóng góp vào công suất bức xạ, chỉ 
liên quan đến sự tích tụ năng lượng ở khu vực bao quanh ngay gần anten, nhưng cần 
được tính đến khi tính trở kháng anten. 
 - Biểu thức của vector Poynting phức, được tính bởi việc sử dụng các 
biểu thức tổng quát của trường sẽ có phần thực (phần liên quan trực tiếp đến bức 
xạ) chỉ bao gồm trường bức xạ cho bởi biểu thức (2.31) 
 __________________________________________________ 
§ 2.4 MỘT SỐ CÁC THÔNG SỐ CƠ BẢN CỦA ANTEN 
Bức xạ của một phần tử dòng điện còn được gọi là bức xạ lưỡng cực. Được dùng 
để định nghĩa các thông số cơ bản của anten nói chung. 
Kiểu bức xạ: 
Phân bố tương đối của công suất bức xạ nnhư là hàm của hướng bức xạ trong 
không gian 
- Công suất bức xạ của dipole nguyên tố tỷ lệ với sin2θ (2.31). Kiểu bức xạ có 
dạng hình số 8 như hình sau: 
 (hình vẽ) 
-a) Mặt 3 chiều 
-b) Mặt E 
-c) Mặt H 
* Tia nửa công suất: Giữa các điểm mà công suất bức xạ = ½ công suất cực đại 
 9
Hệ số định hướng và độ lợi: 
- Các anten thường không bức xạ dồng đều theo mọi hướng. 
- Sự thay đổi của cường độ bức xạ theo hướng không gian được mô tả bởi hàm hệ 
số định hướng D(θ,ϕ) của anten. 
- Cường độ bức xạ là công suất bức xạ góc đặt (hay góc khối). Chính bàng tích của 
vector Poynting với r2. 
- Đối với dipole nguyên tố: (lưu ý (31)) 
( ) 2
2
2
0
2
0
*
32
sin. π
θkdZII
d
dPr l=Ω (2.33) 
Định nghĩa hệ số định hướng: 
( )
r
r
P
d
dP
D Ω= πϕθ 4, (2.34) 
 Với Pr là công suất bức xạ toàn phần. 
- Với dipole nguyên tố: từ (2.33)=> 
( )
π12
. 200
* kdZIIPr
l= (2.35) 
 Vì dΩ =sinθ dθ dϕ. 
Từ (2.33) và (2.34) => 
 (2.36) ( ) θϕθ 2sin5,1, =D
Cực đại đạt giá trị 1.5 khi θ=π/2. 
• Hệ số định hướng cực đại (thường viết tắt là hệ số định hướng) đặc trưng cho 
khả năng của anten tập trung năng lượng bức xạ theo một hướng cho trước. 
• Anten vô hướng: Bức xạ đồng đều theo mọi hướng. 
• Độ lợi G(θ,ϕ)của 1 anten được định nghĩa tương tự như hệ số định hướng, nhưng 
công suất bức xạ đựơc thay bằng công suất toàn phần đặt vào anten Pin. 
• Hiệu suất của anten: inr PP η= (2.37) ( ) ( )ϕθηϕθ ,, GG =• Vậy : (2.38) 
* Effectve isotropic radiated power: (EIRP)=(input power)x(maximum gain). 
chẳng hạn 1 anten có độ lợi =10, công suất nguồn = 1W chỉ đạt hiệu quả như 1 
anten có độ lợi 2 và công suất 5W. Cả hai anten có sùng 1 chỉ số EIRP.vậy có thể 
giảm công suất máy phát nếu sử dụng anten có độ lợi cao. 
* Điện trở bức xạ Ra : 
- Định nghĩa: là điện trở tương đương tiêu thụ cùng 1 lượng công suất như anten 
bức xạ khi dòng cung cấp như nhau. 
- Đối với anten dipode : 
( ) 2
0
2
2
00
a 806
R ⎟⎟⎠
⎞
⎜⎜⎝
⎛== λππ
ll dkdZ
=> (2.39) 
 10
Trong đó: π1200 =Z , 
0
0
2 λπ=k 
Ví dụ: dl = 1m, )1(3000 MHzfm ==λ , Ra = 0,0084 Ω. 
Nhận xét: - Ra thưòng rất nhỏ 
 - T’ỷ lệ thuận với diện tích của anten 
Các anten dipode thường có điện khoáng lớn và hiệu suất thấp, do đó độ lợi thấp. 
Một anten có hiệu suất cao phải có kích thước so sánh được với bứớc sóng. 
Trong dải sóng phát thanh (500-1500kHz, tương ứng 600-200m )cần anten với cấu 
trúc đơn giản như các tháp cao. 
 ______________________________________________ 
§2.5 Bức xạ của vòng điện nguyên tố : 
+ Phân tử dòng bán kính r0, cưòng độ I , trục của phần tử //z. 20.. rdt π
+ Nếu r0 << λ o: nguồn điểm 
+ Phần tử dòng Ùdipode từ với 
 raIrM
2
0π= (2.40) 
+ Vector định hướng của phần tử dòng : '0 ϕdIr
 ( ) Rjkyx eaaRdIrAd 0'''00 cossin4 −+−= ϕϕπ ϕµ 
 Với ( ) ( )[ ] ... ng phẳng với biên độ 
→→−→ rkje)k,(kf yx
→
f , lan truyền theo 
hưóng của vector lan truyền 
→
k . 
* Để ý : 0
222
0
2 kkkkkk yxz ==>−−=
→
* Nếu => hằng số sóng k20
22 kkk xz >+ z là ảo Æ các sóng phẳng trong vùng phổ này 
suy yếu dần theo hướng Z. Nói cách khác, chỉ có cac sóng phẳng trong vùng phổ 
tươnh ứng với mới đóng góp vào trường ở khu xa. 20
22 kkk yx ≤+
* Khi z=0 ta phải có điều kiện biên : 
yx
yjkxjk dkdkeE yx∫ ∫ −−∞
∞
→→ =
-
yxt2 )k,(kf4
1
π
 (5.11) 
Từ ( 5.2 ) ta có : 
 ∫∫ +→→ =
a
yx
S
yjkxjk dydxe .y)(x,E
4
1)k,(kf a2yxt π (5.12) 
* Từ (5.9) => 222
0
..
yx
yyxx
z
tt
z
kkk
fkfk
k
kff −−
−−=−=
→→
 (5.13) 
* Nếu tính được tích phân (5.10) thì xác định được E
r
, nhưng điều này chỉ dễ dàng 
thực hiện khi r>> 0λ hay kor>>1 
Khi đó : )sin.sin,cos.sin(2
cos
00
0
)( 0 ϕθϕθπ
θ kkfe
r
jkE rjkr
→−→ =→ (5.14) 
* Nhận xét : - Trường bức xạ ở khu xa tỷ lệ vói ảnh Fourier của trường ở bề 
mặt với (công thức) là các thành phần của vectorấóng của sóng cầu lan truyền theo 
hướng (θ,ϕ). 
 - Theo hướngZ,fz≈0và cosθ≈1thường bức xạ được tính theo 
(5.14)+(5.12) và đạt cực đại; E
r
chỉ có thành phần Ex,Ey tỷ lệ với fx,fy . 
 - Vì 0. =∇ E
r
 và 0. =fk
rr
 nên thường là đường phân cực ngang TEM 
trong vùng bức xạ (khu xạ) 
 40
_____________________________________________ 
 41
§5.2 BỨC XẠ TỪ MỘT MIỆNG CHỮ NHẬT 
- Giả thiết trường trên miệng là đồng nhất và cho bởi : 
 với 
→→ = xaEE 0
by
ax
≤
≤
 = 0 với các giá trị khác của x,y 
(5.12) trở thành 
 v
v
u
uaabE x
sinsin4f 0t
→→ = (5.16) 
=> Cường độ trường bức xạ được cho bởi (5.15) : 
 )coscos(
sinsin
2
4
00)( θϕπ ϕθ
→→−→ −=→ aa
v
v
u
ue
r
abjkE rjkr (5.17) 
* Nhận xét : 
- (5.17) có dạng tương tự như mảng đồng pha 1 chiều 
- Có dạng tương tự như của kiểu bức xạ trong vùng khả kiến của không gian 
u,v với bkvaku 00 , ≤≤ 
- Các cực đại phụ có độ lớn giảm dần 
* Trong mặt phẳng 0=ϕ : 
( )
θ
θ
π θ sin
sinsin4
2 0
0
0
0
)( 0
ak
akabEae
r
jkE rjkr
→−→ =→ (5.18) 
 Độ rộng tia chính : 
 a
B 0W λθ ≈∆= với 0λ>>a 
 ____________________________________________ 
§5.3 BỨC XẠ TỪ MIỆNG TRÒN 
- Giả thiết trưòng đồng nhất 
 với 
→→ = xaEE 0 222 ayx ≤+
 = 0 với 222 ayx >+
Khi đó : 
θ
θπ
sin
)sin(2f
0
01
0
2
t ak
akJaEa x
→→ = 
 42
Trong đó J0(x) ,J1(x) là các hàm Bessel bậc 0,1 loại 1. 
* J1(x) tương tự như hàm sin tắt dần (hàm lưọng giác có biên độ giảm dần ) 
* Với x>> )
4
sin(2)(
2
1
1
π
π −⎟⎠
⎞⎜⎝
⎛→ x
x
xJ 
* Đồ thị của hàm phương hướngcó dạng tương tự như của bức xạ từ miệng chữ 
nhật, với sự suy giảm nhanh hơn của các cực đại phụ 
 a
B 0832,3W λπθ ≈∆= 
 R = -17,6dB 
 _________________________________________ 
§5.4 MIỆNG VỚI TRƯỜNG ĐỒNG NHẤT 
CÓ PHA BIẾN ĐỔI TUYẾN TÍNH 
Xét miệng hình chữ nhật với cường độ trường có dạng : 
 với 
yjxj
x eaEE
βα −−→→ = 0
by
ax
≤
≤
=> (5.21) dydxeaE
a
a
b
b
ybkjxkj
x
yx .f )()(0t ∫ ∫
− −
−+−→→ = α
=> )cos.sincos())((
)sin()sin(
2
4
00
0000
)( 0 θϕϕπ ϕθ
→→−→ −−−
−−=→ aa
vvuu
vvuue
r
abEjkE rjkr (5.22) 
- Kiểu bức xạ trong hệ toạ độ u,v tương tự như miệng chữ nhật đồng nhất với cực 
đại tại u=uovà v=vo, tức là: 
auak αϕθ == 00 cos.sin 
bubk αϕθ == 00 cos.sin 
=> π
βϕ =tg , ( )
0
2
122
sin
k
βαθ += 
=>có thể điều khiển hướng bức xạ cực đại tương tự mãn 2 chiều. 
* Nếu ß = 0 thì hướng bức xạ cưc đại nằm trong mặt phẳng ϕ = 0( hay mặt phẳng 
xoz) với góc θ = θ0 cho bởi : 
 ⎟⎠
⎞⎜⎝
⎛=⎟⎠
⎞⎜⎝
⎛ παλα 2arcsinarcsin 00k 
 43
- Hướng “không” thoả mãn điều kiện π±=− ouu 
=> ( )
0
0
0 cos
2 θ
λθθ
a
BW =−= 
§.5.5 MIỆNG VỚI TRƯỜNG CÓ BIÊN ĐỘ GIẢM 
TỪ TÂM RA BIÊN: 
xét miệng chữ nhật với phân bố trường có dạng 
)1(0 a
x
aEE x −=
→→
 với 
by
ax
≤
≤
=> 
2
0t
)2(
)2(sinsin2f ⎥⎥⎦
⎤
⎢⎢⎣
⎡
= →→ ak
ak
bk
bk
aabE
x
x
y
y
x (5.23) 
=> 
( )( ) )cos.sincos(22
sinsin
2
00
)( 0 θϕϕπ ϕθ
→→−→ −⎟⎟⎠
⎞
⎜⎜⎝
⎛
=→ aau
u
v
ve
r
abEjkE rjkr (5.24) 
- Tỷ số mức chính trên mức phụ R = 26dB 
- Cực đại chính xảy ra khi u = v =0 
r
abEkE π
00
max
=→ 
--------------------------------------------------------------------------------------- 
 44
CHƯƠNG 6: MIỆNG ỐNG DẪN SÓNG – ANTEN LOA. 
-Miệng ống dẫn sóng( hình chữ nhật hoặc tròn) thường không được sữ dụng làm 
anten phát vì tính định hướng kém, nhưng thường được sữ dụng làm bộ chiếu xạ cho 
anten parabol phản xạ 
§ 6.1 ỐNG DẪN SÓNG CHỮ NHẬT 
 - Xét ống dẫn sóng chữ nhật có kích thước tiết diện ngang là a x b , miệng ống 
định xứ trong mặt z = 0 
- Mode truyền sóng chủ yếu là sóng TE10 (transverse electric), có Ey, Hx, và Hz
 zjy ea
xEE βπ −= cos0 
 zjWx ea
xYEH βπ −−= cos0 (6.1) 
- Với z = 0 => a
xEE y
πcos0= 
 a
xYEH Wx
πcos0−= 
* Tại gần miệng ống xuất hiện sóng phản xạ của mode TE10 và các mode bậc coa 
hơn với biên độ nhỏ 
 * Nếu chỉ sữ dụng miệnh ống dẫn sóng cho bộ chiếu xạ, có thể bỏ qua các mode 
bậc cao và coi trường trong mặt z = 0 , chỉ ≠ 0 trên miệng ống 
- Theo nguyên lý đổi lẫn của 
trường điện từ, có thể coi tồn tại 
dòng từ mặt a
xaEJ xms
πcos0
→→ =
- Tường bức xạ ở khu xạ được tính bởi công thức (5.15) với fx =0 (theo 5.12, lưu ý 
Ex =0) 
( )[ ]( ) ( )[ ]( )220y 2cos2 2
sin
2f
ak
ak
bk
bk
abE
x
x
y
y
−= ππ (6.3) 
- Trong mặt phẳng 
2
πϕ = (yoz) , kx =0, tỷ lệ với θE ( )[ ]( )[ ] θθπ sin2
sin2sin2f
0
0
0y bk
bk
abE= 
- Trong mặt phẳng ϕϕ Ek y ,0,0 == tỷ lệ với 
 45
 ( )[ ]
( )( ) θθπ
θ
cos
sin2
sin2cosf 2
0
2
0
y ak
ak
−
= 
- Công suất bức xạ toàn phần theo (6.2) 
2
04
EYabP Wr = 
 => Hệ số định hướng : 
2
00
2
0
2 64
2
4 λβλπ
θ ab
P
EYr
D
r
== 
* Đánh giá hệ số định hướng: chẳng hạn cho dãi X (8÷12 GHz), 
6.2 ANTEN LOA H 
- Để nhận được trường bức xạ có tính định hướng cao khi so với miệng ống dẫn 
sóng, có thể mỡ rộng các miệng ống dẫn sóngthành các anten loa. 
- Nếu miệng ống dẫn sóng chữ nhật được mỡ rộng trong mpÆanten loa H 
(hình vẽ) 
- Trường bức xạ từ phía miệng ODS về phía miệng loa có dạng mặt sóng trụ tròn 
(hình vẽ) 
- Để trường ở miệng loa gần đồng pha thì góc mở ϕ phải nhỏ. 
- Độ lợi và kiểu bức xạ sẽ giống với miệng bức xạđồng pha, nếu lượng sai khác về 
pha ở rìa miệng loa và tâm loa 
4
π≤ hay 
'444
)( 0120 a
tgRRk λππ ≤⇔≤− 
Vậy để có miệng loa rộng thf góc mở ϕ nhỏÆ hạn chế phạm vi sữ dụng( vì loa 
dài). 
- Nếu bỏ qua sai khác về pha và coi phân bố trường ở miệng loa tương tự như 
trường ở miệng ống dẫn sóng TE10 thì : 
 '
cos0 a
xaEE ya
π→→ = với 
2
'
2
'
by
ax
≤
≤
- Trường bức xạ được tính tương tự trường hợp ống dãn sóng chữ nhật với a Æ a’ 
và hằng số truyền sóng : 
 ( ) 021220 ' kak ≈⎥⎦⎤⎢⎣⎡ −= πβ 
 46
- Hệ số định hướng : 2
0
'2,10 λ
baD = 
- Độ lợi G ≈ D 
- Với cùng 1 chiều dài của loa thì độ lợi sẽ tăng nếu tăng góc mở ϕ. Tuy nhiên khi 
đó sai pha trên miệng loa tăng theo Æ giảm độ lợi 
- Các tính toán lý thuyết Ævới cùng chiều dài loa thì độ lợi cực đại nhận được do 
tăng độ rộng miệng loa a’ cho đến khi sai pha ≈ 0,75 π. 
§ 6.3 MIỆNG ỐNG DẪN SÓNG HÌNH TRÒN 
- Mode TE11 phân bố điện trường trên tiết diện thẳng (sử dụng hệ toạ độ cực ( ϕρ , )) 
 )84,1(
sin2
1 a
JE ρρ
φ
ρ = (5.3.1) 
 ρ
ρ
ϕ
ϕ d
a
dJaE
)84,1(
84,1
cos2 1= (5.3.2) 
(hình vẽ) 
- Trong hệ toạ độ Decarte : 
ϕϕ
ϕϕ
ϕρ
ϕρ
cossin
coscos
EEE
EEE
y
x
−=
−=
 (5.3.3) 
 (hình vẽ) 
- Sử dụng tính chất của hàm Bessel 
 ϕρ 2sin)84,1(2 aJE x = (5.3.4) 
 ϕρρ 2cos)84,1()84,1( 20 aJaJE y −= (5.3.5) 
- Sử dụng công thức tích phân Lommel : 
 u
uJJaae
r
jkE rjk )(
84,1
)84,1(2sin2 11220 0 ϕθ −= (5.3.7) 
 ⎥⎦
⎤⎢⎣
⎡
−=
−
du
udJ
u
Jae
r
jkE rjk )(
)84,1(
)84,1(84,1cos2 122
120 0 θϕ (5.3.8) 
* Nhận xét 
 47
- trong mp 
2
πϕ = (mặt E), kiểu bức xạ tương tự như kiểu bức xạ của miệng bức xạ 
đồng nhất hình tròn (chươnh 4_) 
- trong mp ϕ = 0(mặt H) kiểu bức xạ hoàn toàn tương tự kiểu bức xạ của miệng 
ống chữ nhật. -hệ số định hướng được tìm theo cách tương tự như với ống chữ nhật 
2
0
2
0
66
λ
π
βλ
aD = (5.3.9) 
§ 6.4 LOA H. 
- Để nhận được trường bức xạcó tính định hướng cao hơn so với miệng ống dẫn 
sóng, có thể mở rộng(hay làm loe ra) các miệng ống dẫn sóng thành các anten loa. 
- Nếu miệng ống dẫn sóng chữ nhậtđược mở rộng trong mp H , ta có anten loa H, 
- Trường bức xạ vào loa từ phía miệng ống sẽ có dạng sóng trụ với các mặt đồng 
pha dạng mặt trụ tròn (hình vẽ) 
- Để trường ở miệng loa gần đồng pha thì góc mở ϕ phải nhỏ. 
- Độ lợi và kiểu bức xạ sẽ rất giống với miệng bức xạ đồng pha, nếu lượng sai 
khác về pha ở rìa của loa và tâm loa 
4
π≤ hay 
'444
)( 0120 a
tgRRk λππ ≤⇔≤− 
* Nhận xét : để có miệng loa rộng thì góc mở ϕ phải nhỏ Æ loa dàiÆ giới hạn 
phạm vi ứng dụng. 
- Nếu bỏ qua sự sai khác về pha của trường ở miệng loa thì có thể coi phân bố 
trường ở miệng loa tương tự như trường ở miệng ống dẫn sóng ứng với mode TE10 
,
'
cos0 a
xaEE ya
π→→ = với 
2
2
'
by
ax
≤
≤
- Trường bức xạ dược tính tươnh tựnhư trường hợp miệng ống chữ nhật ở § 5.2 
với aÆa’, với hằng số truyền 0k≈β 
- Hệ số định hướng : 2
0
'2,10 λ
baD = 
- Độ lợi (công thức) 
- Với cùng 1 chiều dài của loa, độ lợi sẽ tăng nếu tăng góc mở. tuy nhiên khi đó sai 
pha trên miệng loa tăng và làm giảm độ lợi. các tính toán lý thuyết đã chỉ ra rằng: với 
cùng 1 chiều dài loa thì độ lợi cực đại nhận được do tăng đọ rộng miệng loa a’ sẽ đạt 
được cho đến khi sai pha ≈ 0,75π. 
 --------------------------------------------------------------------- 
 48
 49
CHƯƠNG 7 : ANTEN PARABOL 
§ 7.1 CẤU TẠO VÀ NGUYÊN LÝ HOẠT ĐỘNG 
- Là anten có tính định hướng tương đối cao, sử dụng chủ yếu ở dải sóng cực ngắn 
(thông tin di đông và vệ tinh) 
- Phương trình mặt parabol trong hệ toạ độ cực: 
θcos1
2
+=
fr (7.1.1) 
- Đặc trưng bề mặt parabol là tất cả các tia bức xạ xuất phát từ từ tiêu điểm (nơi 
đặt loa chiếu xạ ) sau khi phản xạ đều song song với trục parabol Æ có thể áp dụng 
các nguyên lý quang hình để tìm trường trên miệng parabol. 
- Trong các ứng dụng cho nghiên cứu bức xạ vũ trụ, để tránh ảnh hưởng của nhiễu 
từ mặt đất (có thể làm giảm độ nhạy), người ta thường dùng hệ thống chiếu xạ thứ 
cấp. Hệ parabol lúc này được gọi là anten Cassegrain 
 _______________________________________________ 
§ 7.2 Hiệu suất miệng bức xạ 
1) Mật độ công suất bức xạ trên miệng parabol: 
- Ký hiệu g (θ,ϕ): công suất bức xạ/ đơn vị góc đặt theo hướng (θ,ϕ) của nguồn 
chiếu xạ. 
=> công suất đến mặt phản xạ trong góc sinθdθdϕ là : 
ϕθθϕθϕθ ddgPi ..sin).,(),( = (7.2.1) 
- Một công suất tương tự phải xuất hiện trong mặt trên miệng rsinθ dϕ ds 
(công thức) 
2) Tổn hao tràn: đặc trưng bởi hiệu suất tràn: tỷ số công suất được gương phả xạ 
trở lại/tổng công suất bức xạ của bộ chiếu xạ 
 ϕθθϕθρϕθϕρ ddgddrP ..sin).,(..sin),( = (7.2.2) 
 Hay ρ
θϕθϕρ
d
d
r
gP 1),(),( = (7.2.3) 
- Sử dụng (7.1.1) => 
 22
22
4
4cos
ff
ff
+
−=θ (7.2.4) 
( )
222
2
2
2
)4(
16),(
4
cos1),(),(
ff
fg
f
gP +=
+= ϕθθϕθϕρ (7.2.5) 
 50
 Nếu constg =),( ϕθ thì ( )2cos4),( 4 θϕρ =P 
* Hệ số định hướng của bộ chiếu xạ : 
∑
=
×ch
f P
gD )0,0(4π (7.2.7) 
3) Hiệu suất miệng: mô tả tất cả các dạng tổn hao (phân bố biên độ, pha và đặc 
tính phân cực) 
- Trường trên miệng: 
→→→ +== yyxxa aEaEE ),(),(),( ϕρϕρϕρ
- Công suất bức xạ toàn phần từ miệng: giả thiết sóng là sóng phẳng 
 ∫ ∫= π ϕρρϕρ2
0 0
..),(
a
a ddPP
- Mật độ công suất bức xạ trên đơn vị góc đặc : 
22
0 0
2
0
2
022
0 ..),(82
1 ∫ ∫ →= π ϕρρϕρπ
a
a ddE
YkErY (*) 
Nếu công suất bức xạ toàn phần Pa từ miệng parabol được phân bố đồng nhất với 
mật độ Pa / πa2 thì : 
 2
12
0
2 ⎟⎠
⎞⎜⎝
⎛= Ya
PE aa π (**) 
Khi đó trường trên miệng là phân cực thẳng và đồng pha. Trường này tạo ra một 
mật độ công suất trên đôn vị góc dài dọc theo trục z là : 2
22
0
4π
π aPak 
- Thường chiếu thành phần phân cực được sử dụng, chọn thành phần Ey, kh đó: 
 tỷ số công suất bức xạ do thành phần Ey 
Gọi ηλ là hiệu suất miệng ≡ 
 mật độ công suất bức xạ trên đơn vị góc đặc 
∫ ∫
∫ ∫
+
=
→
π
π
λ
ϕρρπ
ϕρρϕρ
η 2
0 0
222
22
0 0
..)(
..),(
a
yx
a
a
ddEEa
ddE
 (7.2.9) 
+ Hiệu suất miệng có thể đựơc biểu diễn bằng tích của 3 số hạng, bao gồm tổn hao 
do chiếu xạ không đồng nhất (1-ηi), tổn hao do sự không đồng pha của trường miệng 
(1- ηp) và tổn hao phân cực ngang (1- ηx), tức là: 
xpiA ηηηη = 
 51
+ Độ lợi trục : 
inin P
I
P
Ig π
π
4
4
== 
Với I: Cường độ bức xạ của anten theo hướng trục (watts/ đơn vị góc đặc) ứng với 
dạng phân cực thẳng cho trước, Pin: công suất đặt vào bộ chiếu xạ. 
+ Công suất bức xạ bởi bộ chiếu xạ : infT PP .η= với fη : là hiệu suất của bộ 
chiấu xạ 
+ Công suất đến miệng parabol là: 
aTS PP =η 
=> 
a
fS P
IG πηη 4..= 
+ Tổng quát : ⎟⎟⎠
⎞
⎜⎜⎝
⎛= 2
0
4.... aIG ipxfS πλπηηηηη 
* Hệ số định hướng: Cường độ bức xạ từ miệng đồng nhất phân cực thẳng: 
θθ ππ
→−→→ == aae
r
EjkEE rjk 200 0
2 
=> Mật độ công suất góc đặc : 
4
0
2
0
2
022
0 82
1 aYEkErY =θ 
+ Công suất bức xạ toàn phần 
2
00
2
2
1 EYaPa π= 
=> )(
4 2
2
0
aD πλ
π= (7.2.10) 
+ Tổng quát : ASaD ηηπλ
π .)(4 22
0
= (7.2.11) 
____________________________________________________ 
 52
CHƯƠNG 8 : ANTEN THU 
§ 8.1 DIỆN TÍCH HIỆU DỤNG 
+ Trong đa số trường hợp, có thể dùng nguyên lý thuận nghịch để khảo sát các đặc 
trưng của anten thu: Các đặc trưng của 1 anten sử dụng để thu sóng điện từ rất gần với 
các đặc trưng tương ứng của anten khi nó được sử dụng để bức xạ sóng điện từ. 
Æ Nếu 1 anten có độ lợi G theo 1 hướng cho trước khi bức xạ sẽ có cùng độ lợi 
như vậy khi nhận bức xạ từ cùng một hướng khi sóng tới có cùng dạng phân cực 
+ Để tiện khảo sát đặc trưng nhận của anten thang ta sử dụng khái niệm diện tích 
hiệu dụng Ae sao cho năng lượng nhận được bởi anten bằng mật độ năng lượng đến 
trên đơn vị diện tích nhân với Ae. 
+ Khi đó nếu điều kiện về dạng phân cực của sóng đến và điều kiện trở kháng 
được thoả mãn thì: 
Gπ
λ
4
A
2
0
e = 
Với anten miệng Ae diện tích thực của miệng ≤
 Và Ae ~ diện tích thực của miệng 
+ Đặc trưng phân cực của 1 anten có thể được mô tả bởi việc sử dụng thông số 
chiều dài hiệu dụng phức h
r
. 
→→= ic EhV .0 trong đó iEr cường độ điện trường sóng tới 
Voc: Thế hở mạch thu được. Với anten dipole 
h
r
~ chiều dài của anten 
nhưng ≤ chiều dài của anten do phân bố dòng bất đồng nhất. 
 ___________________________________________ 
§ 8.2 CÔNG THỨC FRIIS 
- Xét hệ R – T antennas Anten phát có độ lợi Gt (θt ϕt) 
 gọi Pin:công suất đặt vào T – anten 
tΓ : Hệ số phản xạ của đường truyền nuôi T – anten 
=> công suất bức xạ toàn phần là: 
 int P)1(
2Γ− (8.1) 
+ Mật độ công suất trên đơn vị diện tích theo hướng R–anten, ở khoảng cách r sẽ là: 
2
2
4
),(.)1( r
GPP tttintinc π
ϕθΓ−= (8.2) 
 53
=> công suất tín hiệu thu được sẽ là: 
 ),(4
)1)(,()1( 2
22
ttt
in
trrrrrec Gr
PGP ϕθπϕθ Γ−Γ−= (8.3) 
 Công thức (8.3) là công thức Friss 
+ Nếu điều kiện về tính phân cực không thoả mãn thì 
 ),(),(4
)1)(1( 2
2
022
tttrrr
in
trrec GGr
PpP ϕθϕθπ
λΓ−Γ−= (8.4) 
Với : 22
2
.
→→
→→
=
i
i
Eh
Eh
p (8.5) 
 54